Price elasticity is the core of pricing science, as it provides direction on how to adjust and modify historical pricing behavior to achieve P&L objectives. However, estimating price elasticity in B2B contexts is very difficult because of two key issues. First, in B2B contexts, market demand not only is a function of price, but also is affected by many market dynamic factors such as customer size, seasonality, industry, etc. As a result, the relationship between price and quantity must be investigated within each micro-segment to remove the impacts of all other factors and isolate price-related effects. Although market segmentation is an extremely powerful tool to capture market dynamics, it leads to the second issue, data sparsity, which can cause overfitting when estimating price elasticity.
Traditional B2B Elasticity Estimation
Due to the above issues associated with estimating price elasticity, most B2B companies try to set some rules to change their prices based on hypotheses. For example, high velocity products are likely to be more price sensitive than low velocity products, or there is more risk associated with aggressive pricing for customers who spend more than for customers who spend less. As a result, the magnitude of a price change is defined based on combinations of these factors for each segment.
Another approach might be to categorize market segments based on historical price distribution. The main hypothesis here is that if a market segment has a wider historical price distribution, it is less sensitive to price changes, meaning an opportunity exists to increase the price.
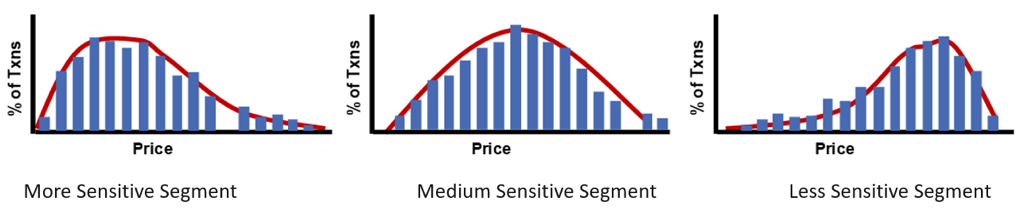
Figure 1: Defined price sensitivity based on historical price distribution.
Data-Driven Price Elasticity
Both approaches fail to reveal the true relationship between price and market demand and to predict the revenue/profit resulting from the recommended price change. Ideally, we should be able to compute the data-driven price elasticity for each segment to be able to predict market demand. Each market segment has it is own sensitivity, but these sensitivities are related because data have a natural hierarchical structure; for example, products belonging to the same categories are supposed to have similar, but not necessarily the same, elasticities. In such cases, two modeling approaches may be taken:
All segments may be modeled together; or Each segment may be modeled separately.
With the first approach, there is a risk of ignoring autocorrelation and identifying one elasticity for groups of segments, which is too general to predict the accurate market demand of each micro segment. With the second approach, there is a risk of ignoring similarity, and data sparsity can be problematic.
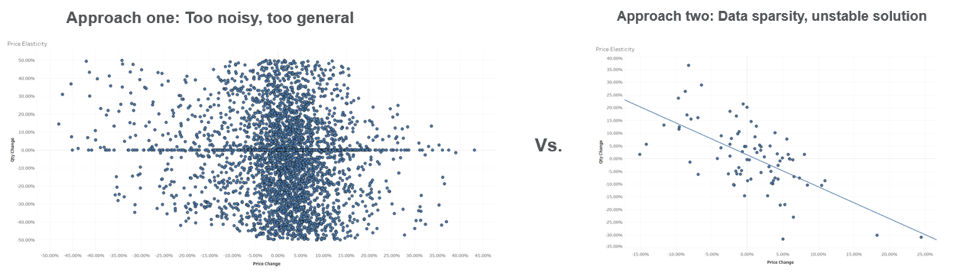
Figure 2: Modeling all segments together vs. each segment individually.
The best approach in such a situation is to develop a hierarchical model with the flexibility to capture and analyze the data structure, and the ability to account for and estimate effects from different segments.Hierarchical models are stronger because data can be analyzed across segments, thereby minimizing the effect of data sparsity. Higher level information can be shared effectively among the lower-level segments, yet lower-level estimation still follows its own data structure and pattern.
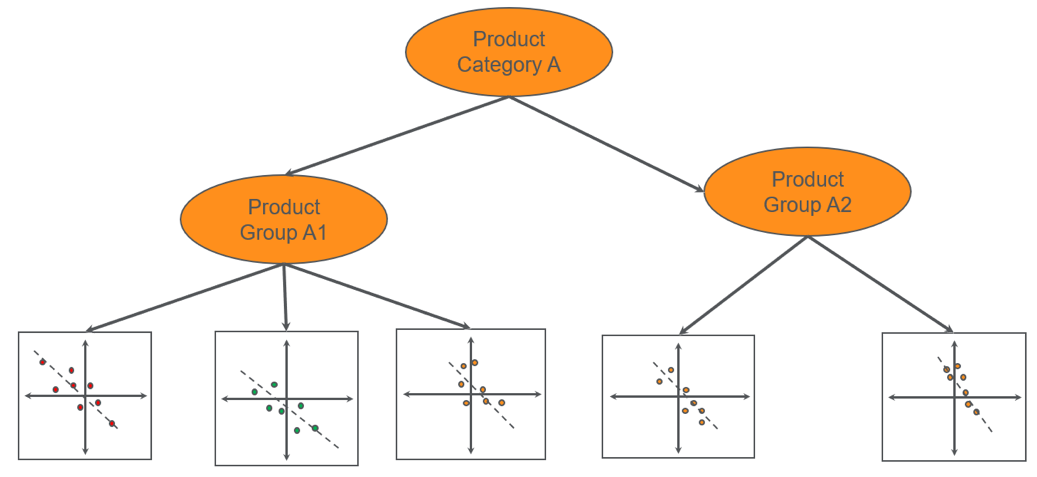
Figure 3: Bayesian hierarchical model to derive price elasticity.
In Figure 3, each product (represented by an individual box) does not have enough data to estimate the relationship between the change in price and change in quantity. A hierarchical Bayesian model can estimate the price elasticity for each product by sharing the information among all products within a product group.
By applying Bayesian hierarchical linear regression modeling to pricing and revenue management, the behavior of every segment is modeled as a linear regression, assuming each has its own unique price elasticity and some similarities in price sensitivity at the group level. The Zilliant approach to price optimization can be employed to derive the price elasticity from hierarchical datasets and deal with data sparsity, reduce noise, and ultimately provide reliable and robust predictions of market demand.
